3041. Asteroids

Bessie wants to navigate her spaceship through a dangerous asteroid field in the shape of an N x N grid (1 ≤ N ≤ 500). The grid contains K asteroids (1 ≤ K ≤ 10,000), which are conveniently located at the lattice points of the grid.

Fortunately, Bessie has a powerful weapon that can vaporize all the asteroids in any given row or column of the grid with a single shot.This weapon is quite expensive, so she wishes to use it sparingly.Given the location of all the asteroids in the field, find the minimum number of shots Bessie needs to fire to eliminate all of the asteroids.

Input. First line contains two integers N and K, separated by a single space. Each line from 2 to K+1 contains two space-separated integers R and C (1 ≤ R, C ≤ N) denoting the row and column coordinates of an asteroid, respectively.

Output. The integer representing the minimum number of times Bessie must shoot.

Пример входа	Пример выхода
3 4 1 1 1 3 2 2 3 2	2

РЕШЕНИЕ

графы – максимальное паросочетание

Анализ алгоритма

В задаче следует найти минимальное покрытие в двудольном графе. Строки сетки представляют левую долю графа, колонки – правую.

Согласно теоремы Кенига оно равно максимальному паросочетанию в двудольном графе.

Пример

Астероиды расположены следующим образом:

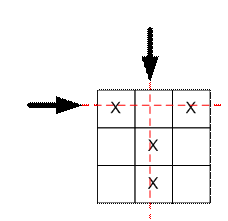
Для уничтожения астероидов Бесси достаточно совершить 2 выстрела.

Максимальное паросочетание (красные ребра) и соответствующее ему минимальное покрытие (зеленые вершины) имеет вид:

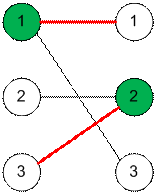
Реализация алгоритма

#include <cstdio>

#include <vector>

#define MAX 510

using namespace std;

vector<vector<int> > g;

vector<int> used, mt, par;

int i, j, ptr;

int n, k, a, b, flow;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = to;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

mt.assign (n+1, -1);

par.assign (n+1, -1);

for (run = 1; run; )

{

run = 0; used.assign(n+1, 0);

for (i = 1; i <= n; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

int main(void)

{

scanf("%d %d",&n,&k);

g.resize(n+1);

for(i = 0; i < k; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

AugmentingPath();

for (flow = 0, i = 1; i <= n; i++)

if (mt[i] != -1) flow++;

printf("%d\n",flow);

return 0;

}